01.06.2011Правило Парето

Принцип Парето: формулировки и сомнения

В литературе по менеджменту (в основном - в популярной или посвященной time-менеджменту) обязательно упоминается так называемый принцип Парето или правило 80/20. Вот некоторые его формулировки:

• 20% клиентов (товаров) дают 80% оборота или прибыли;
• 20% ошибок обусловливают 80% потерь;
• 20% исходных продуктов определяют 80% стоимости готового изделия;
• за 20% расходуемого времени достигается 80% результатов ([1], с.111)
• 80% ваших посетителей смотрит только 20% страниц вашего сайта ([8])
• 20% преступников виновны в 80% преступлений ([7])

Применение этого правила к управлению запасами носит название ABC-анализа (от деления запасов на 3 группы A, B и C, первая из которых находится на постоянном контроле, вторая - на системе периодического дозаказа, а третья планируется и закупается на год. Не путать с ABC - Activity Based Costing, функционально-стоимостным анализом - сокращения одинаковые, сущность разная). Данная система, пожалуй, наиболее разработанное применение правила 80/20 (см. пример в [2], с.177-179). Развернутая история и интерпретация этого принципа содержится в статье [7].

Первоначальная, историческая формулировка - 80% всех богатств принадлежит 20% населения. Именно она встречается в сочинениях Вильфредо Парето, который утверждал, что «способ распределения доходов, по существу, является одним и тем же в разных странах и в различные исторические эпохи» [3]. Согласитесь, это более сильное и более осмысленное утверждение, чем популярный принцип 80/20.

Настораживает и другой факт. Почему в книгах, являющихся энциклопедиями приемов менеджмента ([4], [5]), нет упоминания (во всяком случае, я не нашел) о принципе Парето или правиле 80/20. Чем-то он показался авторам сомнительным, если они решили не включать его в свои книги. В сети есть замечательная статья [6], посвященная анализу применения этого принципа. В ней обращается внимание на то, что в литературе отсутствует масса примеров успешного применения этого принципа. Что-то неладно с этим принципом.

Я намереваюсь показать, что правило 80/20 не укоренено в реальности и имеет чисто психологический характер. Для этого нам понадобятся логика и немного математики - в пределах школьного курса.

Математика и магия чисел

«20% товаров дают 80% прибыли» - очень яркая, запоминающаяся формулировка. 20% товаров дают 100%-20%=80% прибыли. Соответственно оставшиеся 100%-20%=80% товаров дают 100%-80%=20% прибыли. Замечательная кососимметричность! Именно она сделала этот принцип столь знаменитым.

Чтобы разобраться в природе принципа Парето, рассмотрим его математический смысл.

Математическая формулировка

Есть список объектов или видов объектов (товаров) T ₁, T ₂... T _n и есть некоторый измеримый результат (прибыль), который является аддитивной функцией от объектов (общая прибыль является суммой прибылей от всех товаров), R(T ₁,T ₂...T _n)=R(T ₁)+R(T ₂)+…R(T _n). Так вот, принцип Парето гласит:

(1) Существует такое число 0< a<0,5, что объекты можно разбить на две группы M1 и M2 так, что численность группы M1 будет равна a*n, а результат R(M1)=(1- a)*R(M1,M2), т.е. 1- a от общего результата всех объектов,

(2) и при этом a=0,2 (20%).

В такой формулировке видно, что принцип Парето распадается на две части - наличие точки кососимметричности a (точки Парето), и утверждения о значении этой точки a=0,2. Докажем сначала первую часть - что точка Парето существует.

Рассмотрим гистограмму результатов по объектам, предварительно упорядочив по убыванию результата. А теперь построим гистограмму накопленного результата и приблизим ее непрерывным графиком.

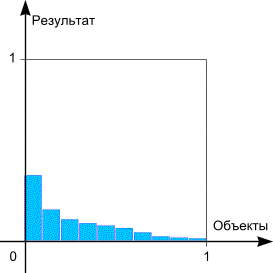
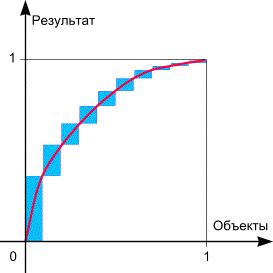
В дальнейших рассуждениях мы будем рассматривать непрерывный график результата, т.е. считаем, что объектов у нас очень много (пример - население страны, несколько тысяч товаров супермаркета). Итак, y=f(x) - график результата, линия красного цвета. График построен в безразмерных единицах - 1 по оси абсцисс соответствует полная совокупность объектов, 100% от их количества; 1 по оси ординат соответствует суммарный результат от полного набора объектов. Где же должна лежать точка Парето? - На прямой y=1-x, именно это равенство выражает искомую кососимметричность, толстая прямая синего цвета.

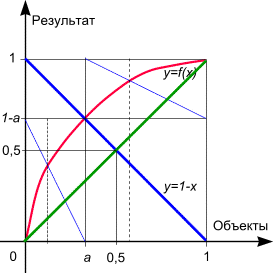
Их пересечение дает искомую точку Парето, точку a, такую, что f( a)=1- a. График y=f(x) строго возрастает, более того - это выпуклая функция (вспоминаем, что объекты мы упорядочивали по убыванию результата, т.е. производная убывает). Отсюда следует, что график функции результата всегда лежит выше прямой y=x (зеленая прямая) и совпадает с ней в одном случае - когда все объекты имеют одинаковый результат, равномерное распределение. Тем самым мы доказали, что искомая точка Парето всегда существует, ее значение меньше 0,5 и равно ему в единственном случае - равномерного распределения результата по объектам.

Из этого графика видно, как мы можем итерационно продолжить Парето-анализ. Если мы рассмотрим ограничение функции на интервале (0, a), то можем построить точку Парето второго порядка (тот же красный график и тонкая синяя прямая; точка Парето-2 показана пунктиром). Аналогично можем поступить на интервале ( a, 1) и так далее.

Магия чисел

Итак, первая часть принципа Парето доказана. Она оказалась на удивление тривиальной - всего лишь иное выражение неравномерности распределения результата по объектам, а в практическом плане - сначала самое важное, потом остальное. Не грех лишний раз напомнить и в этом наибольшая польза этого принципа. Но, может быть, вторая его часть более содержательна? Может, действительно, практически у всех реальных распределений точка Парето равна 0,2? А вот тут мы вступаем в противоречие как с реальными данными, так и с логикой.

Для начала, с чего бы это существенно различным системам иметь какой-то общий для всех, прямо-таки волшебный параметр? Так ли это на самом деле? Обратимся к фактическим данным. На моем рисунке точка Парето примерно равна 0,3, т.е. правило должно бы звучать как 70/30. Но это - так, рисунок с выдуманными данными. А другие примеры? Если обратиться к примеру из книги [2], то числовые данные в приведенной на стр. 178 таблице дадут скорее 75/25, а соответствующий график на стр. 179 - 65/35. Но это - тоже учебные примеры. А вот реальные данные:

• По утверждению Н. Харитонова, КПРФ, 13% населения России владеет 93% ее богатств [6]. Это скорее ближе к 90/10, чем к 80/20;
• Р. Акофф в [12], с. 74 говорит: «Собирая данные для того, чтобы приступить к проблеме прогнозирования, автор обнаружил, что примерно на 10% видов продукции приходится 90% выручки и еще больший процент прибыли»;
• Распределение спроса по наименованиям журналов: доля обращений в зависимости от процента количества журналов по разным электронным журналам дает значение точки Парето от 18 до 28% [13]. Кстати, это действительно достоверное исследование, с внятной методикой и инструментами;
• В статье [11] исследовано применение принципа Парето к заработной плате и выведен несколько шутливый «принцип Парето по-русски» - его численное значение оказалось 86/14, т.е. значение точки Парето равно 0,14.

Как мы видим, значение точки Парето 0,2 - величина очень приблизительная. Казалось бы, велика ли разница между 80/20 и 90/10? - Огромна. Рассмотрим, во сколько раз объект из группы лидеров приносит результата больше, чем из группы аутсайдеров. Оказывается, в (1- a) ²/ a² раз. Для 80/20 это 16, а для 90/10 - 81 раз. Для 70/30 это 70/30 это примерно 5,4 раза. Так что различия - существенные и нельзя говорить, что все эти ситуации описываются примерно одним законом.

Отсюда делаем вывод: 80/20 - это чистой воды магия цифр, к реальности не имеющая большого отношения.

Логическое противоречие

Но расхожие формулировки принципа Парето несут в себе и логическое противоречие. Оно связано с итерационным применением этого принципа. Зададимся вопросом, а может ли существовать такое распределение, такая функция результата, что на любом интервале точка Парето будет постоянна? Пусть это так. Применим этот принцип к интервалам, содержащим точку 0. Получим: f( a)=1- a, f( a²)=(1- a) ², … f( a^k)=(1- a) ^k. Это дает следующее решение: . Интересно отметить, что если мы возьмем последовательность интервалов, сжимающуюся к 1, то получим ту же формулу. Заметим, что у графика этой функции касательная в точке 0 вертикальна, а в точке 1 - горизонтальна. Отсюда получаем противоречие - если взять последовательность интервалов, сжимающихся к другой точке, к примеру, к точке a справа - первый интервал (0, a), потом ( a², a) и т.д., то получим иную формулу - касательная к графику в точке a будет горизонтальна, а для ранее найденной формулы это не так. Значит, не существует такого распределения, такой функции, на которой всегда выполнялся бы принцип Парето с постоянным значением точки Парето.

Математическое доказательство хорошо, но есть и практические противоречия. Для этого сравним принцип Парето с пятым следствием закона Мерфи:

События, предоставленные сами себе, имеют тенденцию развиваться от плохого к худшему.

В чем принципиальное отличие от принципа Парето? В том, что мы можем что-то изменить. Если же следовать букве правила 80/20, то что бы мы ни делали, результат останется тем же! А как еще можно понять, что 20% товаров приносят 80% прибыли? Неужели все менеджеры настолько безграмотны, что не управляют своей сбытовой политикой? Или так безграмотно управляют? Похоже, «собака порылась» в принципе Парето, а не в поведении менеджеров.

Пример из практики - комплектация телевизоров

Но наибольшее противоречие, прямо-таки произвол этого принципа, не в этом. Я наткнулся на него случайно, анализируя различные параметры комплектации телевизоров. Телевизор, согласно комплектовочной ведомости, состоит из примерно 50 частей (не считая радиодеталей, это уже при конвейерной сборке готовой продукции). Вот реальные данные по стоимости по одной из наших моделей:

 

№	Наименование	%	% накопленный Y=f(X)	Линия Y=100%-X
1	323 Кинескоп	51,06	51,06	97,78
2	869 Электронный модуль	16,51	67,57	95,56
3	702 Передняя панель	8,75	76,32	93,33
4	703 Задний корпус	7,10	83,42	91,11
5	890 ПДУ	4,64	88,06	88,89
6	698 Упаковочный ящик из гофрокартона	2,18	90,24	86,67
7	892 Громкоговорители	2,09	92,33	84,44
8	731 Пеновкладыши	2,05	94,38	82,22
9	891 Петля размагничивания	1,60	95,98	80,00
10	73 Плата кинескопа в сборе	1,30	97,28	77,78
11	913 Держатель кинескопа металлический	0,62	97,90	75,56
12	701 Блок кнопок управления	0,34	98,24	73,33
13	896 Прокладка резиновая под кинескоп Т2	0,31	98,55	71,11
14	903 Прокладка резиновая 30х30х9 мм	0,20	98,75	68,89
15	4686 Направляющая передняя вспомогательная	0,12	98,87	66,67
16	699 Сетевая кнопка	0,12	98,99	64,44
17	920 Пакет полиэтиленовый для ТВ	0,11	99,10	62,22
18	4685 Провод монтажный	0,10	99,20	60,00
19	4688 Прокладка резиновая 25х7 мм	0,09	99,29	57,78
20	700 Блок световодов	0,09	99,38	55,56
21	1136 Гайка М6	0,08	99,46	53,33
22	4689 Жгут ОС	0,07	99,53	51,11
23	911 Шайба металлическая зубчатая	0,06	99,59	48,89
24	893 Батарейки диоксид-марганцевые	0,05	99,64	46,67
25	4687 Направляющая задняя поддерживающая	0,05	99,69	44,44
26	918 Инструкция по эксплуатации ТВ	0,04	99,73	42,22
27	897 Прокладка из стекловолокна	0,03	99,76	40,00
28	1008 Опора трансформатора пластм.	0,03	99,79	37,78
29	716 Талон гарантийный	0,03	99,82	35,56
30	899 Ярлык пластиковый AV самоклеящ. задний	0,02	99,84	33,33
31	898 Стяжка пластмассовая 2,5х95 мм	0,02	99,86	31,11
32	905 Держатель шнура питания пластм.	0,02	99,88	28,89
33	1009 Наклейка фирменная на короб	0,02	99,90	26,67
34	895 Лента самоклеющ. 150х19х0,3 мм	0,01	99,91	24,44
35	919 Пакет полиэтиленовый для аксессуаров	0,01	99,92	22,22
36	914 Шильдик "Полар" алюминевый	0,01	99,93	20,00
37	901 Ярлык пластиковый AV самоклеящ. боковой	0,01	99,94	17,78
38	915 Пружина винтовая 6ммХ40	0,01	99,95	15,56
39	888 Схема принципиальная-чертеж ТВ	0,01	99,96	13,33
40	2363 Этикетка самокл. штрих-код	0,01	99,97	11,11
41	900 Ярлык пластиковый (номер модели)	0,01	99,98	8,89
42	906 Переходник сетевого выключателя пластм.	0,01	99,99	6,67
43	2289 Гарантийная пломба	0	99,99	4,44
44	916 Пружина винтовая 0.7X10X18mm	0	99,99	2,22
45	917 Наклейка самоклеящ. цвет корпуса	0	100,00	0,00

В последних двух столбцах содержатся данные для вычисления точки Парето. Видим, что пересечение достигается на пятой позиции, a=0,11. Тут действует правило 89/11, а не 80/20. Казалось бы, все понятно. Но в оперативном управлении (в основном, в логистических задачах - доставка, растаможка, складирование) мы не анализируем комплектацию по полусотне позиций. Для этих целей большинство этих позиций объединяется в одну - «мелочевка». Посмотрим, как изменится значение точки Парето после группировки:

№	Наименование	%	% накопленный Y=f(X)	Линия Y=100%-X
1	Кинескоп	51,06	51,06	87,50
2	Электронный модуль	16,51	67,57	75,00
3	Передняя панель	8,75	76,32	62,50
4	Мелочевка	7,71	84,03	50,00
5	Задний корпус	7,10	91,13	37,50
6	ПДУ	4,64	95,77	25,00
7	Упаковочный ящик	2,18	97,95	12,50
8	Пеновкладыши	2,05	100,00	0,00

Теперь картина изменилась просто кардинально. Пересечение уже в районе точки a=0,3, правило приобретает вид 70/30. Задумаемся над этим изменением.

Разве как-то изменилась реальность? - Нет, она осталась прежней. В чем же фокус? - Изменилась модель реальности. Вместо физических объектов считаем их группы, т.е. абстракции. А разве до того были физические объекты? Ведь часть из этих деталей идет не по одной штуке (общее количество деталей с учетом количества для данной модели составляет 280, и это без учета саморезов и стяжек). Расписав все по физическим объектам, мы могли бы получить и правило 99/1.

Заметим, что операциями дробления и объединения мы можем почти произвольно сдвигать значение точки Парето в любую сторону. Какой-то странный этот принцип Парето, который так сильно меняется от точки зрения.

Ложные следствия и ограничения правила Парето

Ложные следствия

Одной из особенностей принципа Парето является то, что он в силу своей хлесткой красоты способствует ложным из него выводам. К примеру, в одной из студенческих работ в сети (жаль, не сохранил ссылку) встретил замечательную рекомендацию отказаться от 80% товаров, которые дают всего-то 20% прибыли. Автор свысока своего студенческого знания обвиняет предпринимателей в незнании этого принципа и нежелании увеличить свою прибыль! Или, к примеру, бездумное итеративное применение этого принципа приводит к заключению ([9]), что 49% усилий дают 99% результата. Воистину, стоит немного подумать о естественных ограничениях этого принципа, о его области релевантности.

Многокритериальность

Прежде всего, даже если принцип Парето верен, то он говорит об оценке по одному параметру. Пусть даже 20% товаров приносят 80% прибыли и дохода, но для прибыли и дохода это, скорее всего, разные группы товаров. Близкий мне пример - затраты на погрузку в порту пропорциональны весу товара, затраты на транспортировку и складское хранение пропорциональны его объему, таможенные платежи пропорциональны стоимости товара, время работы декларантов на растаможку (и, соответственно, вероятность ошибок) пропорционально количеству позиций в инвойсе, время разгрузки на склад примерно пропорционально количеству коробок. Если обратиться к ранее рассмотренному примеру (см. п.2.4), то кинескопы попадают в лидеры по стоимости, весу, объему, а мелочевка - в аутсайдеры по этим позициям. Если же посмотреть на время работы декларантов и на время разгрузки машины, то ситуация прямо противоположная - с кинескопами все просто-быстро, а с мелочевкой куча проблем. Так что принцип Парето в данном случае лишь частный прием в решении отдельных аспектов логистических задач, на что-то глобальное он не тянет.

Если обратиться к финансам, то только очень простой бизнес управляется на основе одного показателя. Как правило, этих показателей 5-8, так что и здесь принцип Парето не станет чем-то глобальным. А как частный случай, как прием - сначала обращать внимание и усилия на самое важное, на лидеров - да, работает, и хорошо работает.

Неаддитивность

Как мы видели в математической формулировке (см. п.2.1), существенным условием является аддитивность функции результата. То есть объекты должны быть независимы. Всегда ли это так на самом деле? 80% прибыли дают 20% товаров. Почему магазины не откажутся от остальных 80% товаров? - А вы пойдете в такой магазин? Мои потребности явно не ограничиваются самым необходимым, я хочу иметь возможность купить то, что мне нужно (пусть это и не самый ходовой товар). Если магазин откажется от этого товара, то я скорее пойду в другой магазин, даже если там все немного дороже. То есть продажи товаров не всегда независимы! И что, бедные владельцы магазинов не могут ничего сделать? - Разумеется, могут. Они закажут меньше неходовых товаров (оптимизация запасов), установят на них бо'льшую наценку (помните о многокритериальности? Неходовой товар может стать более прибыльным - недаром в маркетинге есть стратегия «падающего лидера», когда на ходовой товар резко снижается цена, это увеличивает поток покупателей, которые раскупают и менее ходовые товары с большей наценкой).

Это лишь один пример неаддитивности. А вот другой - скорость работы конвейера определяется продолжительностью самой долгой операции. Упорядочим операции по времени выполнения и займемся лидерами. Пусть мы расшили узкие места (распараллелили или усовершенствовали технологию) и время выполнения этих операций сократилось в 5 раз. Неужели конвейер стал работать в 5 раз быстрее? Скорее всего - нет, просто теперь скорость его работы определяется другими операциями. Здесь работает иная стратегия - нам не надо максимального сокращения длительности конкретной операции, нам надо приемлемое сокращение. У конвейера обычно есть какие-то железные ограничения - для сборки телевизоров это длина линейки прогрева и нормы времени на прогрев. Мы легко можем поделить время прогрева на максимальное количество телевизоров на линейке прогрева и получим физическое ограничение такта конвейера. Тут принцип Парето может быть применим к ранжированию проблем, но важно другое - напрямую длительности операций этому принципу не подчиняются.

Те же соображения применимы и для скорости транспортной колонны, и для обеспечения безопасности - не стоит ставить бронированные ворота с вооруженной охраной фасада, если сзади есть неохраняемая деревянная дверь с амбарным замком. Тот же принцип достижения не максимального, а приемлемого результата.

Вообще говоря, здесь работает именно иной базовый принцип, не принцип Парето - для системы, чей вход непрерывен, а выход дискретен, необходимо добиваться не максимальных, а приемлемых решений. Абитуриенту, поступающему в университет, надо набрать определенный проходной балл - это не значит, что ему надо стремиться получить по всем предметам максимальные оценки. К примеру, он может рассчитывать получить по сочинению (даже не знаю, сейчас на экзаменах его пишут?) любую оценку кроме двойки, а большинство баллов набрать на профильных предметах. Поэтому он может свой непрерывный ресурс (время на подготовку к экзаменам) распределить между предметами соответствующим образом.

Крайняя степень неаддитивности - продукцию можно произвести, только если есть ВСЕ комплектующие. Не важно, сколько стоит/весит/занимает объема деталь, но если ее нет, то конвейер будет стоять. Тут в принципе работает не сложение, а логические операции.

Неопределенность во времени

Отдельного обсуждения требует неопределенность будущего. Я на этом много останавливаться не буду, отсылаю к замечательной статье [6]. Основная ее мысль - сегодняшние аутсайдеры могут стать будущими лидерами. Некоторый аналог принципа Парето в этом плане - матрица БКГ ([4], с.167-168, [5], с.279-280), в последнее время подвергается обоснованной критике (см. [10]).

Интересно сопоставить принцип Парето с принципом Эйзенхауэра (см. [1], с.118-120) в time-менеджменте. В первом один критерий, во втором - два (важность и срочность). Со вторым принципом у меня всегда были проблемы - некоторые дела все же надо делать сейчас, иначе они потом вырастут в большие проблемы. Как их классифицировать? Срочные, но не важные, или важные, но не срочные? Наверное, часть так, часть так. Пожалуй, оптимальный портфель дел по Эйзенхауэру должен состоять из важных, но не срочных и срочных, но не важных. При таком портфеле любую задачу можно поручить, всегда будет время на важные дела, а некоторыми не важными в крайнем случае можно пожертвовать. А что покажет тут принцип Парето? По срочности - одно, по важности - противоположное. Этот пример показывает, что даже более развернутая модель (двухпараметрическая) вызывает проблемы с классификацией, так как же может эта система управляться однопараметрическим критерием?

Еще один временной аспект - в экономических системах классификация параметров зависит от временного масштаба. К примеру, в краткосрочном плане затраты на бухгалтерию являются условно-постоянными, а в долгосрочном плане - переменными. Если мы планируем открыть еще один цех или крупный склад, то потребуется увеличение штата бухгалтеров на обработку операций, затраты на бухгалтерию становятся переменными - они зависят от объема бизнеса. В пределе все затраты являются переменными - на уровне решения вопроса, каков должен быть масштаб бизнеса и стоит ли этому бизнесу существовать.

Как это связано с принципом Парето? Вот как - результаты Парето-анализа, примененные к разным временным масштабам, могут противоречить друг другу. Если помнить, что принцип Парето есть не более чем частный инструмент, вроде умения находить максимум функции с помощью производной, то все в порядке. А вот если возвести его в глобальный принцип - жди беды.

Доказательство верности правила 80/20

А теперь, когда мы рассмотрели и раскритиковали принцип Парето, нашли в нем логические противоречия, докажем его верность именно в изначальной постановке, как правило 80/20.

Группировка объектов

Мы работаем не с реальностью, а с моделями реальности. И эти модели несут в себе отпечаток не только реальности, но и нашей психики. Одним из таких психологических источников является закон 7±2. Посмотрите на большинство круговых диаграмм в литературе или используемых в вашей работе. Как правило, они имеют от 5 до 9 секторов, редко больше. Посмотрите на многоуровневые классификаторы товаров или материалов в учетных программах. Те из них, которые правильно организованы, удобны персоналу, имеют на каждом уровне до двух десятков значений (кроме нижнего уровня). Слишком подробная информация неудобна для анализа, точность должна быть минимально достаточной.

Еще одна особенность - группировка часто предшествует сбору данных. В п.2.2приводились статистические данные по распределению богатства населения России. Напомню, 13% населения владеют 93% богатств. Почему такие странные цифры - 13 и 93? Логичнее бы звучало, что 10% населения владеют 91% богатств, или 20% населения владеют 99% богатств. Почему обе цифры не круглые? Потому, что это след от предварительной группировки населения. Сначала все население по каким-то признакам было разбито на группы, а уж потом оценивался размер этих групп и размер богатств, им принадлежащих. Важно отметить, что часто группировка осуществляется на основе качественной модели системы, и лишь потом измеряется количественно. А создание качественных систем во многом искусство, часто это не формализуемый процесс.

Неизмеримость и недостаток информации

Все, кто проводил социологические опросы, знают, что результаты существенно зависят от постановки вопроса. В результате получаются количественные данные, но что они описывают? Как правило, некоторый сплав представления о ситуации исследователя (вопросы) и респондентов (ответы). Реальность они описывают только тогда, когда у исследователя адекватная модель этой реальности и правильно сформулированы вопросы. Да и то, это искаженное описание реальности. Экономика (а социальные науки - тем более) тем и отличается от математики, что изначально работает с неполными и не достаточно достоверными данными.

Можно группировать людей по первой букве фамилии (нормальная модель для словаря или библиотечного каталога), но узнать распределение доходов людей по буквам алфавита вряд ли возможно иначе, как получить полный список людей и их доходов и потом совершить группировку. Беда в том, что у нас нет и никогда не будет столь полных данных. А часть данных вообще невозможно измерить количественно, тем более - заранее. Как можно оценить эффект от какого-либо дела, особенно если оно личного плана. В чем он выражается? - Только качественно, «большой», «средний», «незначительный». Можно, конечно, этим оценкам приписать какие-то числовые значения, но будут ли они суммироваться? Равняются ли пять незначительных эффектов одному среднему? Или двум?

Психологическое доказательство верности правила 80/20

Один пашет, а семеро руками машут

В чем же мы ошибались, когда рассматривали математическую формулировку принципа Парето? Мы упустили из виду операцию группировки. Эта операция существенно влияет на один из исходных параметров - количество объектов. Как мы видели в практическом примере (см. п.2.4), операция группировки меняет значение точки Парето с 0,11 на 0,3, что очень существенно. Как уже отмечалось (см. п.4.1), мы работаем с моделями реальности. А эти модели мы строим сообразно нашему разуму, а не только сообразно реальности. Поэтому мы группируем объекты в 7±2 групп, причем делаем это при каждой итерации Парето-деления. Тем самым исходная математическая формулировка не верна - на каждой итерации мы работаем с новыми объектами, не унаследованными с предыдущей итерации, т.е. с новой моделью. Теперь можем сформулировать психологическую формулировку принципа Парето:

Из 7±2 объектов (групп, дел) 1-2 заслуживают нашего особого внимания (приносят основной результат).

В такой формулировке значение точки Парето находится как раз в пределах 0,1-0,25, что примерно соответствует правилу 80/20. В этой формулировке становится понятно, почему принцип Парето в основном упоминается в книгах по time-менеджменту - неопределенности в оценке важности дел и потребного на них времени настолько велики, что этот принцип не поддается точной количественной проверке. А как наглядный стимул он работает что надо. Думаю, любой рекламщик отдал бы мизинец, лишь бы придумать столь яркий слоган.

Заключение. Принцип Дисбаланса

Принцип Парето, или правило 80/20, имеет еще одно название - принцип Дисбаланса. Обычно он звучит так:

Большая часть усилий пропадает зря.

Более вредное утверждение трудно придумать! Вы этому верите? Если да, то ваша картина мира явно одномерна. Любая сложная система описывается набором параметров. Глупо думать, что каждый из них распределен по всей системе равномерно, на каких-то элементах достигается максимум. Но еще глупее думать, что максимум по всем параметрам достигается на одних и тех же элементах.

К примеру, возьмем какой-нибудь боевик, где небольшая группа спецназа в тылу врага идет на задание. Если это правильно подобранная группа, то умения членов этой группы далеко не однородны. Пусть они распределены так, как показано в таблице.

 

	Рукопашный бой	Стрельба	Знание языков	Скалолазание	Компьютер
Джо	5	2	1	4	0
Билл	2	2	2	3	4
Грег	2	5	1	2	1
Адам	2	4	3	2	2
Сэм	4	1	1	5	1
Дик	1	2	2	1	5
Чарли	2	1	5	1	1
Тэд	2	3	4	1	1

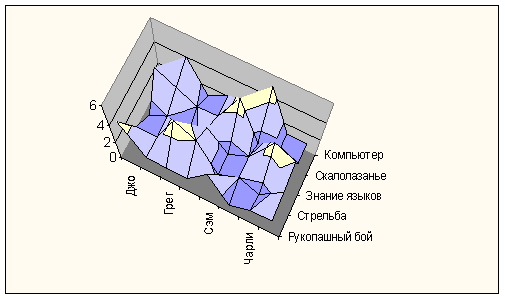
Если проанализировать по Парето по любому из параметров - что рукопашный бой, что стрельба - то состав группы явно не оптимален. Вроде как лишние люди. Но если посмотреть на группу в целом, то по любому параметру достигается максимум. И из таблицы, а особенно на объемном графике (см. ниже), видно, что все максимумы достигаются на разных людях (вершины показаны бледно-желтым цветом). Более подробный анализ показывает, что максимум не один, есть резерв (для спецназа это уж точно необходимо).

Психологи знают, что именно такой состав небольшой группы дает психологическую устойчивость - каждый член группы в чем-то лучший, каждый пользуется заслуженным уважением. То же самое про распределение максимумов различных параметров можно сказать о любой достаточно сложной системе - если она действительно система, т.е. ее элементы взаимосвязаны.

 

Вильфредо Парето был гораздо мудрее своих последователей, когда говорил, что неравномерность распределения доходов неизбежна. Это следствие того, что мы работаем со сложной системой. В конце концов, деньги - это всего лишь один из параметров жизни, важный, но не единственный важный.

Таким образом, принцип Парето, правило 80/20 - лишь локальный прием, вроде нахождения локального максимума с помощью производной. Для поиска глобального максимума одного параметра не достаточно. Кстати, равномерное распределение параметра может говорить как о том, что максимум достигнут, так и о том, что система не зависит от этого параметра.